Reibung und Erwärmung
Reibung und Verschleiß
Die Reibung beschreibt die Kraft, die der Bewegung entgegenwirkt. Als Kenngröße wird der Reibungskoeffizient μ angegeben.
Die Reibung ist im Wesentlichen abhängig von folgenden Einflussfaktoren:
- Gleitpaarung
- Belastung
- Gleitgeschwindigkeit
- Lagertemperatur
- Schmierungszustand
- Beschaffenheit der Gleitflächen.
Prinzipieller Verlauf des Reibungskoeffizienten
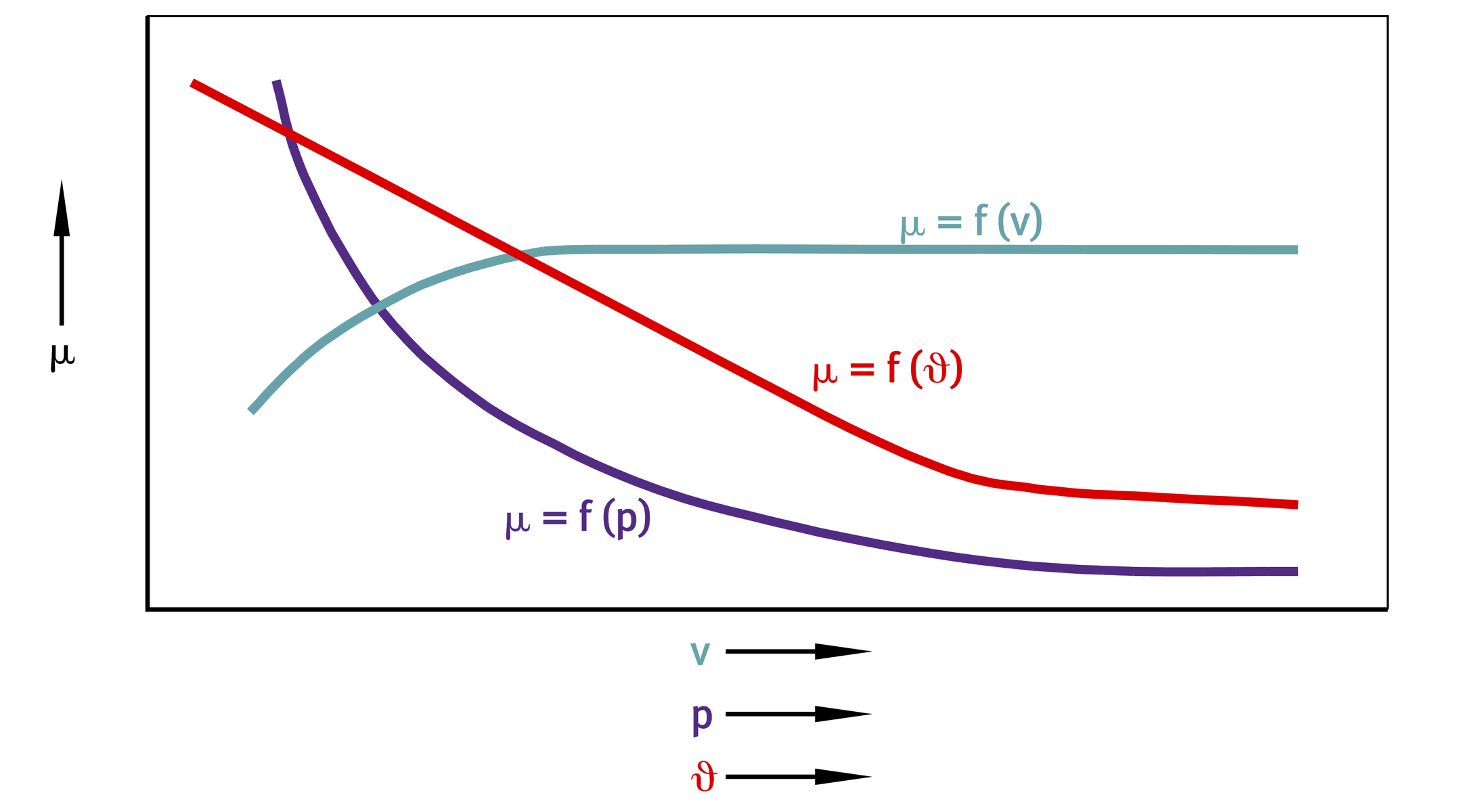
Für wartungsfreie Gleitlager auf Basis von PTFE ist der prinzipielle Verlauf des Reibungskoeffizienten μ in Abhängigkeit von Gleitgeschwindigkeit, Belastung und Temperatur dargestellt, ➤ Bild. Der Reibungskoeffizient sinkt mit steigender spezifischer Lagerbelastung p und sinkender Gleitgeschwindigkeit v.
Reibungskoeffizient, prinzipieller Verlauf
Verschleiß- und Reibungsverlauf
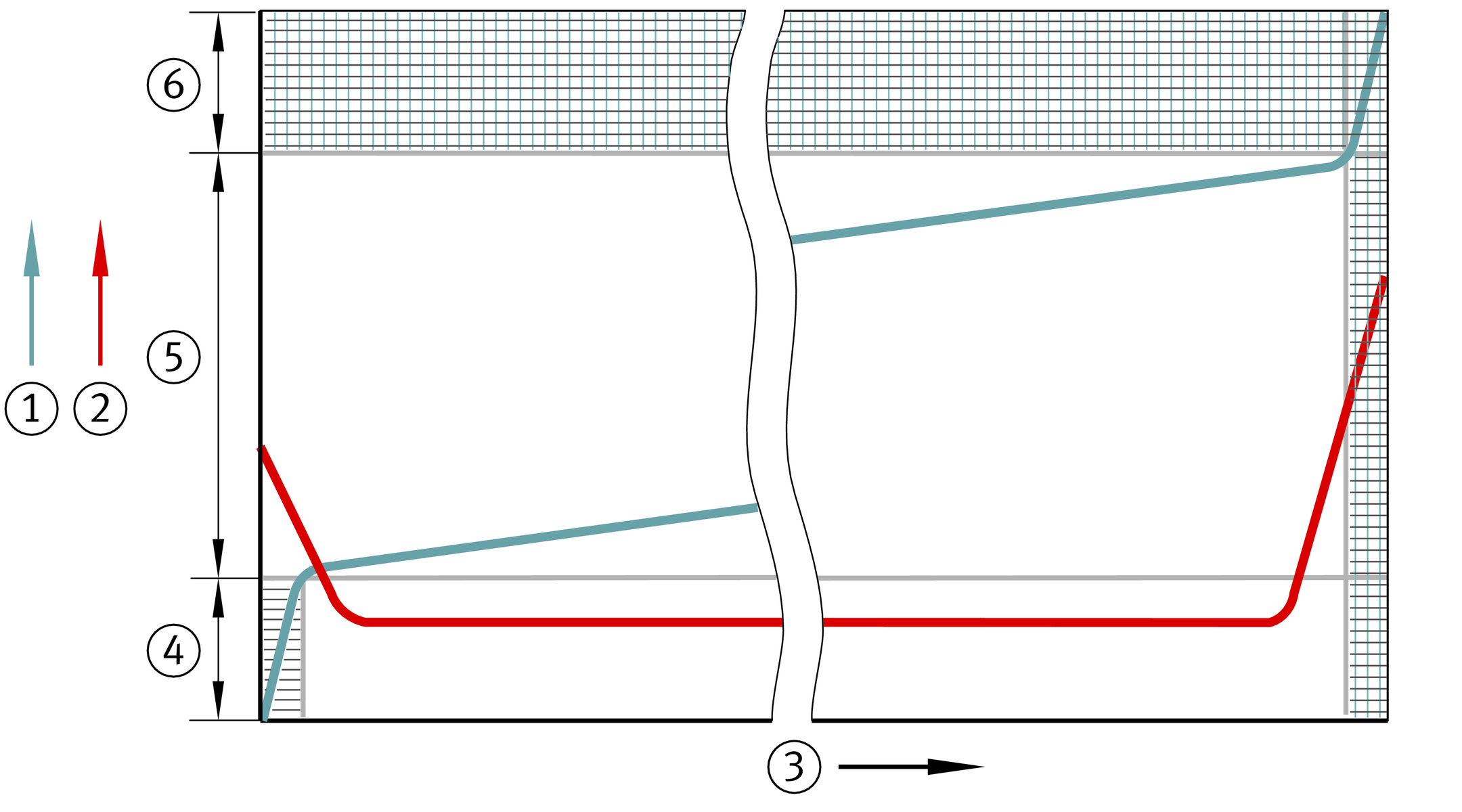
Der Verschleißverlauf von wartungsfreien Gleitlagern unterteilt sich in Einlaufphase, Hauptverschleißphase und Ausfallphase, ➤ Bild. Die Hauptverschleißphase verläuft annähernd linear.
Der Reibungsverlauf von wartungsfreien Gleitlagern hat ebenfalls in den drei Phasen einen charakteristischen Verlauf, ➤ Bild.
Verschleiß- und Reibungsverlauf






Lagerreibmoment
Das Lagerreibmoment M gilt bei Radial- und Schräg-Gelenklagern sowie bei Buchsen bei radialer Belastung. Bei Axial-Gelenklagern und Anlaufscheiben gilt dies für die axiale Belastung.
Bei neuen Gleitlagern kann in der frühen Einlaufphase das Lagerreibmoment deutlich höher sein. Die Gründe hierfür sind:
- Plastische Anformung des PTFE-Werkstoffes an die Oberflächenstruktur der Gegenlauffläche
- Die noch nicht erfolgte Lagereigentribologie, das Absetzen von PTFE-Partikeln auf die Gegenlauf- und Funktionsfläche (PTFE-/PTFE-Reibung).
ACHTUNG
Werden Gelenklager kombiniert radial und axial belastet, ist das Lagerreibmoment M durch Integration der Normalkräfte zu ermitteln! Bei Bundbuchsen muss das Reibmoment sowohl für die radiale Gleitfläche als auch für die axiale Gleitfläche am Bund berechnet werden!
Die Angaben zu Reibungskoeffizienten gelten für Gleitlager ohne Dichtungen 2RS, 2TS, 2RS2 oder 2RS4. Bei Gleitlagern mit Dichtungen erhöht sich das Reibmoment des Lagers abhängig von der Dichtungsausführung enorm.
Berechnung
Das Lagerreibmoment M wird ermittelt nach: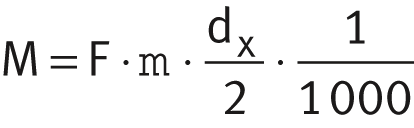
| M | Nm | Lagerreibmoment |
| F | N | Zentrisch wirkende radiale oder axiale Kraft |
| μ | – | Reibungskoeffizient, siehe Tabelle |
| dx | mm | Spezifischer Durchmesser, siehe Tabelle. |
ACHTUNG
Zur Berechnung der Antriebsleistung ist aus Gründen der Sicherheit immer der maximale Reibungskoeffizient einzusetzen, siehe Tabelle! Liegt der Reibungskoeffizient über dem Maximalwert, so kann sich der Verschleiß erhöhen, die Lagertemperatur steigen und die Funktion des Gleitlagers beeinträchtigt werden!
Spezifischer Durchmesser
Gleitlager | Spezifischer Durchmesser dx |
|---|---|
Radial-Gelenklager | dK |
Axial-Gelenklager | 0,7 · dK |
Schräg-Gelenklager | 0,9 · dK |
Buchse | Di |
Bundbuchse (radiale Gleitfläche) | Di |
Bundbuchse (axiale Gleitfläche) | Dfl |
Anlaufscheibe | Do |
Vergleich der Reibungskoeffizienten
Gleitschicht, Gleitpaarung | Gegenlauffläche | Reibungskoeffizient μ | |
|---|---|---|---|
min. | max. | ||
E40** | Stahl | 0,03 | 0,25 |
E50 | Stahl | 0,02 | 0,2 |
ELGOGLIDE | Hartchrom | 0,02 | 0,2 |
ELGOGLIDE-W11 | Hartchrom | 0,02 | 0,15 |
ELGOTEX | Stahl | 0,03 | 0,2 |
PTFE-Verbundwerkstoff | Hartchrom | 0,05 | 0,2 |
PTFE-Folie | Stahl | 0,05 | 0,2 |
Stahl/Stahl | 0,08 | 0,22 | |
Stahl/Bronze | 0,1 | 0,25 | |
**Die detaillierten Reibungskoeffizienten für E40 beachten.
Wärmeabfuhr
Reibung wird in Wärme umgesetzt. Wesentlich für die Funktion eines Gleitlagers ist die ausreichende Wärmeabfuhr. Sie erfolgt durch Konvektion über die Gehäuse und Wellen an die Umgebung. Gegebenenfalls wird Wärme über den Schmierstoff abtransportiert.
Gleitlager, in denen eine hohe Reibenergie pv umgesetzt wird, benötigen eine erhöhte Wärmeabfuhr.

